Dalam soal ini kita disuruh untuk mencari perbandingan dari jumlah dan selisih kedua vektor tersebut.
Harus dicari satu per satu dulu.
Soal :
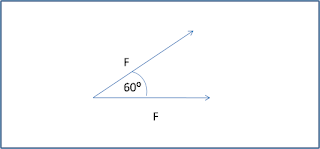
1. Dua buah vektor besarnya sama dan membentuk sudut 60⁰. Berapakah perbandingan antara jumlah dan selisih kedua vektornya?
Nah, sekarang kita cari jumlahnya dulu. Setelah itu barulah mencari selisihnya, sehingga hasil akhirnya bisa kita dapatkan.
Jumlah kedua vektor
Gambar kedua vektor bisa dilihat diatas.
Selisih kedua vektor
Untuk mencari selisih, rumus yang digunakan adalah seperti ini.
Perbandingan jumlah dan selisih
Untuk mendapatkan perbandingannya, kita tinggal bagi saja antara jumlah dan selisihnya.
Jadi perbandingan antara jumlah dan selisih kedua vektor itu adalah √3
Soal :
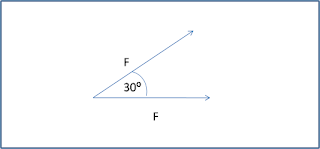
2. Dua buah vektor besarnya sama dan membentuk sudut 30⁰. Berapakah perbandingan antara jumlah dan selisih kedua vektornya?
Caranya masih sama dengan soal pertama..
Jumlah kedua vektor
Untuk mencari jumlahnya, kita gunakan rumus :
Selisih kedua vektor
Gunakan rumus ini!!
Harus dicari satu per satu dulu.
Soal :
1. Dua buah vektor besarnya sama dan membentuk sudut 60⁰. Berapakah perbandingan antara jumlah dan selisih kedua vektornya?
Nah, sekarang kita cari jumlahnya dulu. Setelah itu barulah mencari selisihnya, sehingga hasil akhirnya bisa kita dapatkan.
Jumlah kedua vektor
Gambar kedua vektor bisa dilihat diatas.
- besar keduanya sama, kita misalkan dengan F
- sudut yang mengapitnya adalah 60⁰
Untuk mencari jumlahnya, kita gunakan rumus :
R² = F₁²+ F₂² + 2. F₁.F₂.Cosα
- F₁ dan F₂ besarnya sama, yaitu F
- α = 60⁰
R² = F₁²+ F₂² + 2. F₁.F₂.Cosα
R² = F²+ F² + 2. F.F.Cos60
- cos 60 = ½
R² = 2F² + 2. F². ½
R² = 2F² + F²
R² = 3F²
- untuk mendapatkan R, akarkan 3F²
R = √(3F²)
R = √3.√F²
- akar F² adalah F
R = F√3
Selisih kedua vektor
Untuk mencari selisih, rumus yang digunakan adalah seperti ini.
S² = F₁²+ F₂² - 2. F₁.F₂.Cosα
- F₁ dan F₂ besarnya sama, yaitu F
- α = 60⁰
S² = F₁²+ F₂² - 2. F₁.F₂.Cosα
S² = F²+ F² - 2. F.F.Cos60
- cos 60 = ½
S² = 2F² - 2. F². ½
S² = 2F² - F²
S² = F²
- untuk mendapatkan S, akarkan F²
S = √F²
- akar F² adalah F
S = F
Perbandingan jumlah dan selisih
Jadi perbandingan antara jumlah dan selisih kedua vektor itu adalah √3
Soal :
2. Dua buah vektor besarnya sama dan membentuk sudut 30⁰. Berapakah perbandingan antara jumlah dan selisih kedua vektornya?
Caranya masih sama dengan soal pertama..
Jumlah kedua vektor
Untuk mencari jumlahnya, kita gunakan rumus :
R² = F₁²+ F₂² + 2. F₁.F₂.Cosα
- F₁ dan F₂ besarnya sama, yaitu F
- α = 30⁰
R² = F₁²+ F₂² + 2. F₁.F₂.Cosα
R² = F²+ F² + 2. F.F.Cos30
- cos 30 = ½√3
R² = 2F² + 2. F². ½√3
R² = 2F² + √3F²
R² = F²(2+√3)
Selisih kedua vektor
Gunakan rumus ini!!
S² = F₁²+ F₂² - 2. F₁.F₂.Cosα
- F₁ dan F₂ besarnya sama, yaitu F
- α = 30⁰
S² = F₁²+ F₂² - 2. F₁.F₂.Cosα
S² = F²+ F² - 2. F.F.Cos30
- cos 30 = ½√3
S² = 2F² - 2. F². ½√3
S² = 2F² - √3F²
S² = F²(2-√3)
Baca juga :




Post a Comment for "Dua Buah Vektor Besarnya Sama dan Membentuk Sudut 60 derajat. Berapa Perbandingan Jumlah dan Selisih Kedua Vektor Itu?"